Have you ever wondered how scoring in Elasticsearch is done?
Or you might be wondering why Solr ranked your results in a particular order.
Do you understand what happens under the hood? Both these systems use Apache Lucene internally. Now Lucene does scoring using a combination of Boolean Model on the inverted index and Vector Space Model.
In the previous article, we learned the Boolean model on an inverted index. It is used to shortlist documents that match our query. This list is then scored and sorted in decreasing order of relevance using the Vector Space Model. This article explains how the search scoring algorithm works using the vector space model in information retrieval by simplifying the terminologies and jargon.
How the search scoring algorithm selects the documents that will be ranked
When we get a free text query, it can be converted into a boolean query using any of the boolean operators. E.g. the query: “Vector Space Model” and be converted to the query “Vector” OR “Space” OR “Model”. We know how to use an inverted index to find documents matching this boolean query. This is explained in the previous article.
Once we have a list of documents that match our query, we try to rank these documents. To achieve this we use the Vector Space Model. To understand this model, we first need to understand what vectors are.
What are Vectors and Vector Space?
Vector
According to Wikipedia, a vector is a quantity that has both magnitude and direction. The direction component can be treated as a dimension of a vector. For eg, we can represent a point in geometry in vector notation. The directions or dimensions can be its length in the x-axis and y-axis. The exact quantity of this length is called the magnitude of that dimension. E.g point (2,3) can be represented as 2*x + 3*y
Vector Space
Vector space can be considered as the imaginary space where all vectors that are being represented using similar dimensions can be thought to exist. In this space, we can add, subtract or multiply the vectors with each other
Term vector
But what does this mean in our context? How can vectors be used to rank results? Simply stating, we want a way using which we can represent our queries and documents in mathematical notation. In the context of information retrieval, what we are more interested in is term vectors.
Term Vectors are used to represent statistics like the frequency of each term in our query or document. For eg, we can consider each term as a dimension of the vector and the frequency of each term as its magnitude. Once we have the dimension and magnitude known, then this query can be represented in our vector space. Our vector space is composed of all the vectors that can be formed using any of the words present in our documents.
For example. the query: “Eye for an Eye” can be represented as the following vector: 2*(Eye) + 1*(for) + 1*(an). Here the words in parenthesis are the dimensions of the vector and the numbers are the magnitude of each dimension which in this case is just the frequency of the word in our query.
Assigning Weights to Vectors
Now that we know what term vectors are, the natural question arises, how can this be used to rank results? The answer to this lies in assigning the correct magnitude a.k.a weight to each query or document vector. If we assign correct weights, then the problem of ranking documents reduces to performing some mathematical operations on the vectors of each document and the vector of our query. The result of the operations is our score representing how relevant the document is to the query. The ranking then simply means sorting the list of matching documents in decreasing order of score.
So let’s try to understand how we find the magnitude of each dimension of our term vectors. The weight is composed of two components:
- Term Frequency
- Inverse Document Frequency
Term Frequency – Prioritizing documents that contain query words more times.
Suppose there are two documents that contain the words of our query. We will naturally want that the documents containing words in the query more number times to be considered more important than the documents where the words occur fewer number times. Term Frequency component of weight allows us to achieve this. The higher the number of times the term occurs in our query or document, the higher its term frequency.
Inverse Document Frequency – Reducing the impact of common words
Using just the term frequency alone has a problem. Consider the words that occur very frequently in our language. For eg consider the word “the“. This word would occur in almost all documents of reasonable length. But it does not mean if this word is present in our document we consider that document more relevant. Now consider the word “Vector“. Not all documents will have this word. But the documents that do contain this are more relevant to our query “The Vector Space Model”. So if a word is occurring in all the documents, we want to give it lower importance in ranking. Conversely, the words that are rare should add more weight to the ranking. To do this we use Inverse Document Frequency.
To calculate inverse document frequency, we count the number of documents that contain this word. This is known as document frequency for the term. Since we want common words to have less impact and rare words to have more impact, we invert the document frequency.
Inverse Document Frequency = 1/document frequency
Once we have term frequency and inverse document frequency, we can give the weight using the formula:
Weight = TF * IDF
where TF is the number of times a term occurs in the document or query.
and IDF = Inverse Document Frequency of Term
If we use this formula for weights in our term vectors, we give more impact to the words that occur more times in the document while minimizing the impact of words that are common in all documents.
Score calculation using Term Vectors
Now that we have correct weights assigned to our vectors, the search scoring algorithm is ready to calculate the score. To do this, we first create a term vector of our query. Also, remember we already had the list of documents matching the query using boolean retrieval. Now for each document in the list, we create its term vector. Now we need to perform a mathematical operation between our query vector and the vector of each document in the list. The result of each operation is the score for that particular document to query pair.
There can be different mathematical functions used to calculate the similarity score. The one that is most commonly used is known as Cosine Similarity.
Cosine Similarity – How similar are the documents to queries?
Cosine similarity calculates how similar two vectors are. It is measured by the cosine of the angle between two vectors and represents whether two vectors are pointing in roughly the same direction.
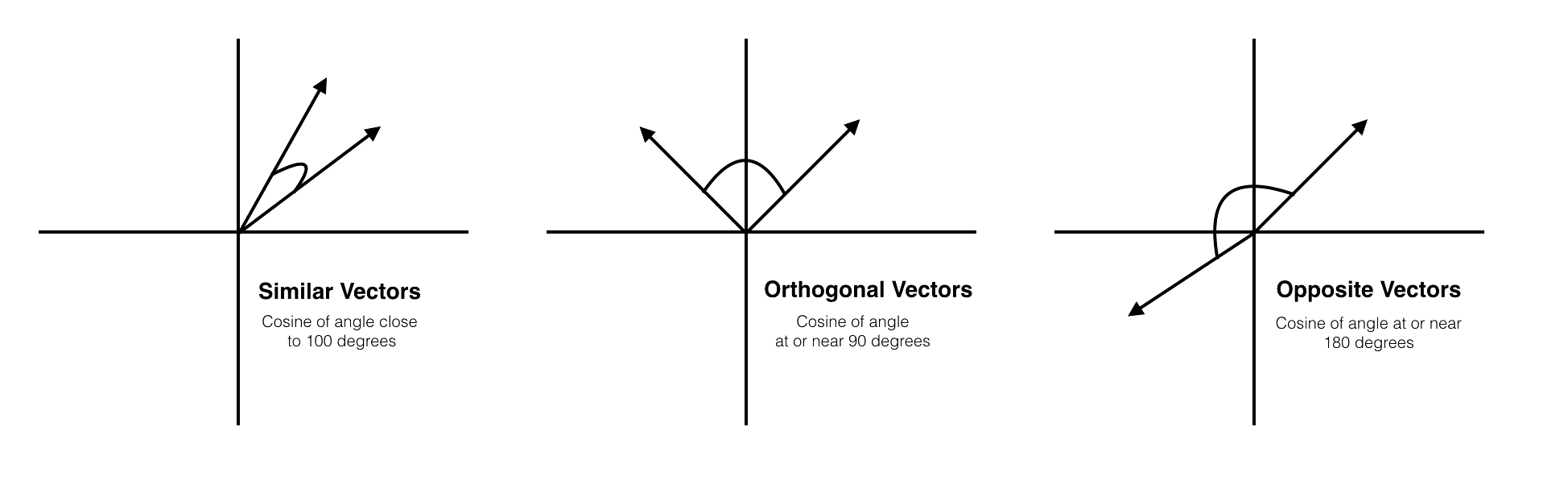
Cosine similarity is calculated using the following formula:
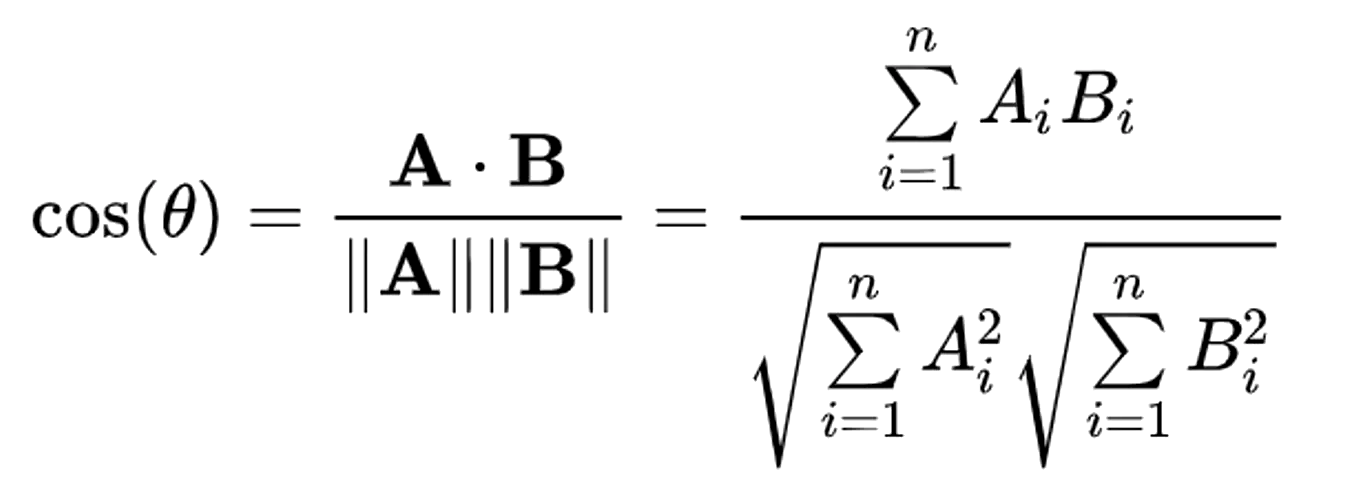
The result of this operation is our score. Once we have scored each document, we sort our list of matching documents according to the score. The documents that have more terms in common with our query will rank higher. Similarly, the documents that have fewer terms will rank lower.
Conclusion
In this article, we understood the inner workings of the search scoring algorithm. We learned what vectors are. We then understood how to represent queries and documents as vectors. After that, we used the cosine similarity formula to find the score of the documents to query. At last, we understood that we can use this score to rank documents. This in a nutshell explains how the Vector Space model is used in Information Retrieval to calculate scoring. This is the model that is used in Lucene and hence in Solr and Elasticsearch.
Hope you learned something from this article. What next?
In this article, we learned how search results are scored, but how to find out the list of search results for which we need to calculate the score? This is done in a fast and efficient manner using the inverted index data structure. Read all about it here.
